Function notation is a fundamental concept in mathematics, enabling clear representation of relationships between variables. It simplifies expressions and equations, making them easier to interpret. This notation is widely used in algebra, calculus, and real-world applications, providing a standardized way to communicate mathematical ideas effectively. Understanding function notation is essential for advanced problem-solving and forms the basis for more complex mathematical concepts.

Evaluating Functions
Evaluating functions involves substituting specific input values into a function to find the corresponding output. This process is essential for understanding function notation and solving algebraic problems effectively.
2.1 Evaluating Functions with Given Inputs
Evaluating functions with given inputs is a straightforward process that involves substituting specific values into the function’s variable. For example, if you have a function f(x) = 4x ౼ 7 and you need to evaluate it at x = 3, you would replace x with 3 and perform the arithmetic operations. This results in f(3) = 4(3) ౼ 7 = 12 ౼ 7 = 5. The process ensures that you can determine the output of a function for any valid input within its domain.
Worksheets often provide practice problems where students are given functions and input values, such as g(x) = 2x + 5 or h(x) = x/2 + 3, and are asked to compute the results. Understanding this concept is crucial for advanced topics like composite functions and inverse functions. By mastering evaluation with given inputs, students build a strong foundation in function notation and its applications. This skill is essential for solving real-world problems and interpreting mathematical relationships effectively.
2.2 Evaluating Functions with Variable Inputs
Evaluating functions with variable inputs involves substituting expressions or variables into the function’s rule. For instance, if the function is defined as f(x) = 3x + 2, and the input is x = y ⸺ 1, the evaluation would be f(y ౼ 1) = 3(y ⸺ 1) + 2 = 3y ⸺ 3 + 2 = 3y ౼ 1. This process allows for expressing outputs in terms of another variable or expression, which is useful in solving equations and understanding relationships between variables.
Worksheets often include problems where students must evaluate functions with inputs like 2x, x + 3, or h(a). This skill is crucial for composite functions and inverse functions, as it requires understanding how functions transform inputs. By mastering this concept, students can solve complex problems and interpret function behavior effectively. It also prepares them for real-world applications where variables represent dynamic quantities. Evaluating functions with variable inputs enhances algebraic manipulation skills and logical thinking.

Domain and Range in Function Notation
The domain of a function is the set of all input values for which the function is defined. The range is the set of all output values. Both concepts are essential for understanding function behavior and restrictions.
3.1 Finding the Domain of a Function
Finding the domain of a function involves identifying all possible input values (x-values) for which the function is defined. This is crucial for understanding the function’s behavior and limitations. For polynomial functions, the domain is typically all real numbers, as they are defined for any x-value. However, for rational functions, the domain excludes values that make the denominator zero, as division by zero is undefined. Radical functions, such as those with square roots, require the expression inside the radical to be non-negative, further restricting the domain. Additionally, functions with even roots, like square roots, may have more stringent requirements than those with odd roots. Understanding how to determine the domain is essential for graphing functions and solving real-world problems. By analyzing the function’s structure, such as identifying denominators, radicals, and other restrictions, you can accurately determine its domain and express it in interval notation.
3.2 Determining the Range of a Function
Determining the range of a function involves identifying all possible output values (y-values) it can produce. Unlike the domain, which focuses on input restrictions, the range highlights the function’s output capabilities. For linear functions, the range is typically all real numbers, unless restricted by the function’s definition. For quadratic functions, the range is determined by the vertex, either opening upwards or downwards, creating a minimum or maximum value. Rational functions may have ranges influenced by horizontal asymptotes, while radical functions often omit certain y-values based on the domain’s restrictions. To find the range, analyze the function’s behavior, consider its type, and identify any vertical asymptotes or turning points. The range is often expressed in interval notation and is crucial for understanding the function’s output limitations. Accurately determining the range is essential for graphing and interpreting functions in various mathematical and real-world contexts.

Composite Functions
Composite functions involve combining two or more functions, where the output of one function serves as the input for another. This concept is essential for modeling complex processes and solving real-world problems effectively.
4.1 Definition and Examples of Composite Functions
A composite function, also known as a composition of functions, occurs when the output of one function is used as the input of another. It is formally defined as (f ∘ g)(x) = f(g(x)), where f and g are functions. This concept allows for the creation of more complex functions by combining simpler ones.
For example, if f(x) = x² and g(x) = 3x + 1, then the composite function (f ∘ g)(x) would be f(g(x)) = (3x + 1)². Expanding this gives 9x² + 6x + 1. Composite functions are essential in modeling real-world phenomena, such as calculating distances or transforming data. They also appear frequently in calculus for differentiation and integration purposes.
Another example involves functions with different operations. If f(x) = sin(x) and g(x) = 2x, then (f ∘ g)(x) = sin(2x), which is a common waveform in physics and engineering. Understanding composite functions is crucial for solving problems in various fields and simplifying complex mathematical expressions.
Practice worksheets often include exercises where students evaluate composite functions at specific points, ensuring mastery of this fundamental concept. Composite functions demonstrate how mathematical operations can be layered to create sophisticated models, making them a cornerstone of advanced problem-solving.
4.2 Evaluating Composite Functions
Evaluating composite functions involves substituting values into the combined functions. Given two functions f(x) and g(x), the composition (f ∘ g)(x) = f(g(x)) requires evaluating g(x) first, then plugging the result into f(x). For example, if f(x) = x² and g(x) = 3x + 1, then (f ∘ g)(2) = f(g(2)) = f(7) = 49.
When evaluating composite functions, it’s crucial to follow the order of operations. Mistakes often occur when the inner and outer functions are confused. For instance, (f ∘ g)(x) is not the same as (g ∘ f)(x). Worksheets with answers provide practice in such scenarios, ensuring clarity and accuracy.
Evaluating composite functions is essential in various applications, such as modeling real-world phenomena or solving complex equations. Mastery of this concept is vital for advanced mathematical problem-solving, and practice worksheets are an excellent tool for achieving proficiency.
Function Notation in Word Problems
Function notation is a powerful tool for solving word problems by translating real-world scenarios into mathematical expressions. It helps in defining relationships between variables succinctly. For instance, if a problem states, “The cost of producing x units is $50x + $2000,” this can be written as C(x) = 50x + 2000, where C represents the cost function.
Word problems often require identifying the independent and dependent variables. For example, “The distance traveled by a car in t hours at 60 mph” can be expressed as d(t) = 60t. Worksheets with answers provide numerous exercises to practice such translations, ensuring students master the skill of converting verbal descriptions into function notation.
Mastering function notation in word problems enhances problem-solving abilities and prepares students for advanced mathematical modeling in fields like physics, economics, and engineering.
Graphical Interpretation of Functions
Function notation helps in graphing functions, revealing key features like max points and symmetry. For quadratic functions, such as modeling a basketball’s path, it visually represents the function’s behavior and outcomes.
6.1 Plotting Functions Using Function Notation
Plotting functions using function notation involves translating algebraic expressions into visual graphs. This process helps identify key features such as the vertex, direction, and intercepts of the function. For example, quadratic functions like f(x) = ax² + bx + c can be plotted by identifying the vertex and determining the parabola’s opening direction. Linear functions, such as f(x) = mx + b, are simpler, with straight-line graphs that show a constant slope. Function notation also aids in identifying intervals where the function is increasing or decreasing, which is crucial for analyzing real-world applications. By plotting points and connecting them, students can visualize how inputs and outputs relate, making abstract concepts more tangible. This skill is essential for understanding function behavior and solving practical problems, such as modeling the trajectory of a basketball or analyzing economic trends.
6.2 Identifying Key Features of Functions
Identifying key features of functions is essential for understanding their behavior and graphical representation. These features include the domain, which defines the input values for which the function is valid, and the range, which specifies the possible output values. Additionally, identifying intercepts (x-intercepts and y-intercepts) helps determine where the function crosses the axes. For quadratic functions, finding the vertex reveals the maximum or minimum point, while for rational functions, vertical and horizontal asymptotes are critical. Understanding these elements allows for accurate graphing and analysis. For example, in quadratic functions like f(x) = ax² + bx + c, the vertex form f(x) = a(x ⸺ h)² + k provides direct insights into the parabola’s direction and vertex location. These skills are vital for interpreting and solving real-world problems, such as modeling projectile motion or optimizing economic functions.
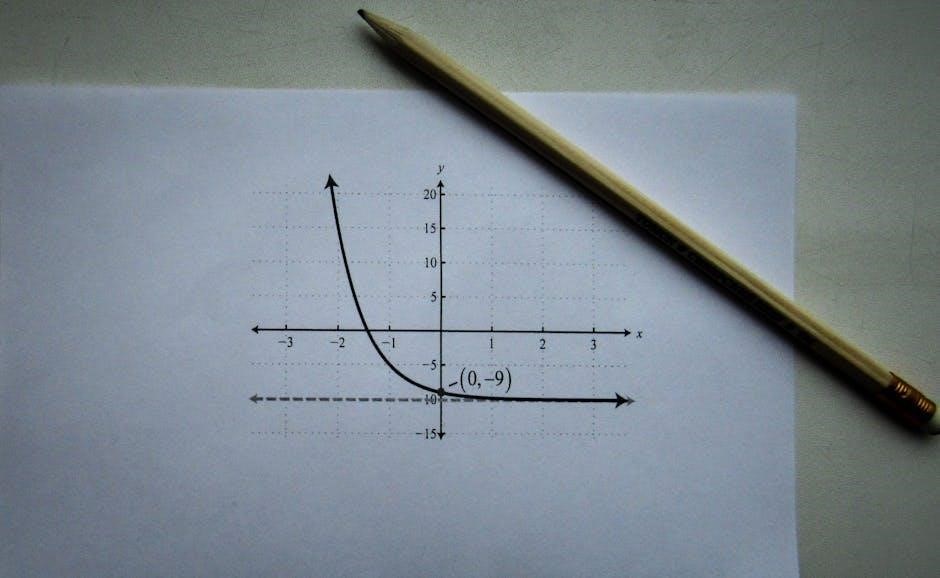
Inverse Functions
Inverse functions reverse the action of the original function, denoted as f⁻¹(x). They satisfy the property f(f⁻¹(x)) = x and are essential for solving equations and real-world problems involving reversibility and symmetry.
7.1 Finding the Inverse of a Function
Finding the inverse of a function involves reversing the mapping of the original function. To find the inverse, start by replacing f(x) with y, then swap x and y, and finally solve for y. This process effectively undoes the action of the original function. For example, given f(x) = 2x + 3, replacing f(x) with y gives y = 2x + 3. Swapping x and y results in x = 2y + 3. Solving for y yields y = (x ౼ 3)/2, so the inverse function is f⁻¹(x) = (x ౼ 3)/2. It’s important to verify that the inverse function satisfies f(f⁻¹(x)) = x and f⁻¹(f(x)) = x. This ensures the correctness of the inverse. Inverse functions are crucial in solving equations and real-world problems involving reversibility, such as temperature conversions or financial calculations.
7.2 Verifying Inverse Functions
Verifying inverse functions involves checking that two functions are true inverses of each other. To confirm, we use the composition of functions. If f(g(x)) = x and g(f(x)) = x, then f and g are inverses. For example, if f(x) = 2x + 3 and g(x) = (x ౼ 3)/2, we verify by composing them. Calculating f(g(x)) gives f((x ⸺ 3)/2) = 2*((x ౼ 3)/2) + 3 = x, and g(f(x)) = g(2x + 3) = (2x + 3 ౼ 3)/2 = x. Both compositions yield x, confirming the functions are inverses. This verification ensures that each function reverses the effect of the other, which is essential for solving equations and modeling real-world phenomena. Always check both compositions to confirm the inverse relationship, as one composition alone does not suffice.
Applications of Function Notation in Real-World Scenarios
Function notation is widely applied in real-world scenarios to model and analyze relationships. In physics, it describes motion, such as the trajectory of a basketball thrown from the free-throw line, represented by a quadratic function. In economics, functions like the Leontief production function illustrate input-output relationships in manufacturing. Temperature conversion formulas, such as F(C) = (9/5)C + 32, are everyday examples of function notation in action. Additionally, function notation is used in nutrition to calculate caloric needs based on variables like weight and activity level. For instance, the Mediterranean diet often uses functions to balance macronutrient intake. These applications demonstrate how function notation provides a clear, interpretable framework for solving real-world problems. By expressing complex relationships mathematically, functions enable precise predictions and optimizations across diverse fields. This practical relevance underscores the importance of mastering function notation for both academic and professional success.
Practice Worksheets with Answers
Printable worksheets on function notation are available, offering timed exercises for skill mastery. They include 10 problems each, covering basic, intermediate, and advanced levels, with detailed solutions provided for self-assessment.
9.1 Basic Function Notation Problems
This section provides foundational exercises to help learners grasp the essentials of function notation. Problems include evaluating functions at specific points, such as finding ( f(10) ) or ( g(-2) ), and determining the domain of simple functions like ( f(x) = x + 4 ) or ( g(x) = 2x ⸺ 3 ). Additionally, learners are introduced to defining and interpreting functions, ensuring a clear understanding of input-output relationships. The exercises also cover identifying whether a relation represents a function and solving basic composite function problems. Each worksheet includes 10 problems with step-by-step solutions, allowing students to verify their answers and improve their skills. These problems are designed to build confidence and prepare learners for more advanced function notation challenges. The focus is on clarity and precision, ensuring a solid mathematical foundation.
9.2 Intermediate Function Notation Problems
This section offers more challenging exercises to deepen understanding of function notation. Problems include evaluating composite functions, such as ( f(g(x)) ) and ( g(f(x)) ), and finding the inverse of functions. Learners also practice determining the domain and range of more complex functions, including piecewise and quadratic functions. Additionally, exercises involve solving equations using function notation and interpreting real-world applications, such as modeling population growth or financial transactions. The worksheets include 10 problems per set, with detailed solutions provided to aid self-study. These intermediate problems build on basic concepts, introducing scenarios that require critical thinking and application of multiple skills. By mastering these exercises, students develop a stronger grasp of function notation and its practical uses in various mathematical contexts.
9.3 Advanced Function Notation Problems
This section presents challenging exercises designed for advanced learners, focusing on intricate function notation concepts. Problems involve evaluating multi-step composite functions, such as ( f(g(h(x))) ), and solving for inverse functions in complex scenarios. Students are tasked with determining the domain and range of higher-degree polynomials and rational functions, as well as analyzing piecewise functions with multiple conditions. Additionally, exercises include solving systems of equations using function notation and interpreting advanced real-world applications, such as modeling population dynamics or optimizing economic functions. The worksheets provide 10 advanced problems per set, with detailed solutions to guide learners. These problems require a deep understanding of function properties and their applications, preparing students for higher-level mathematics and practical problem-solving. By mastering these advanced exercises, learners enhance their analytical and critical-thinking skills in manipulating and interpreting functions.
Solutions and Explanations
This section provides detailed solutions and step-by-step explanations for all practice problems. It addresses common mistakes, offering corrections and clarifications to ensure a thorough understanding of function notation concepts and applications.
10.1 Detailed Solutions for Practice Problems
This section offers comprehensive step-by-step solutions for all function notation problems. Each solution is clearly explained, ensuring understanding and mastery of key concepts. For example, problems involving evaluating functions at specific inputs are solved by substituting values into the function and simplifying. Composite functions are addressed by breaking down the process into manageable steps, such as evaluating inner functions first before applying the outer function. Common mistakes, like misapplying operations or misunderstanding domain restrictions, are highlighted and corrected. Additionally, solutions for finding the domain and range are provided with detailed explanations, often using interval notation for clarity. Visual aids, such as graphs and tables, accompany complex problems to enhance comprehension. By walking through each problem methodically, learners can identify their errors and improve their problem-solving skills effectively.
10.2 Common Mistakes and Corrections
When working with function notation, common mistakes often arise from misunderstandings of substitution, domain restrictions, and composite functions. One frequent error is incorrectly substituting values into functions, such as misapplying operations or ignoring order of operations. For example, evaluating f(x) = 2x + 3 at x = 4 should yield 11, not 10. Another mistake is assuming all functions are defined for all real numbers, ignoring domain limitations like square roots or denominators. Additionally, students often confuse composite functions, such as f(g(x)) versus g(f(x)), leading to incorrect results. To avoid these errors, carefully substitute values, check domain restrictions, and apply functions in the correct order. Practicing with multiple problems and reviewing solutions can help identify and correct these common pitfalls, improving overall proficiency in function notation.
Tips for Mastering Function Notation
Mastery of function notation requires consistent practice and a deep understanding of its underlying principles. Start by thoroughly grasping the basics of functions, such as domain, range, and evaluation. Regularly practice substituting values into functions and interpreting their results. Use worksheets and online resources to reinforce your skills, focusing on both numerical and algebraic inputs. Pay attention to composite functions and inverse functions, as they often pose challenges. Solve real-world problems to see the practical applications of function notation, which can enhance your understanding. Review common mistakes, such as misapplying operations or ignoring domain restrictions, and learn from them. Seek feedback from teachers or peers to identify areas for improvement. Finally, stay organized and methodical in your approach, breaking down complex problems into manageable steps. With dedication and persistence, you can confidently master function notation and apply it effectively in various mathematical scenarios.

